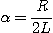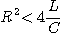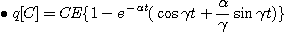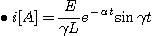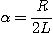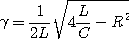|
|
1) 평형방정식 |
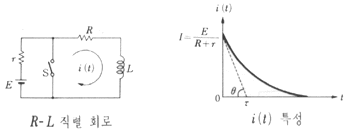
1. 스위치가 열려있는 경우의 평형 방정식
2. 스위치가 닫힌 경우의 평형방정식
|
2) 전류
|
1. 그림에서 스위치를 닫을 때의 전류는스위치를 닫았을 때 평형방정식은
변수분리법에 의하여
t = I = 0 이라 하면,
따라서 2. 그림에서 스위치를 열 때 흐르는 전류스위치가 열려있을 때의 평형방정식은
정상전류는 0 이고 변수분리법에 의해서
이것을 다시 쓰면
초기조건은 t=0에서 i=E/R 이라 하면
3. R-L 직렬회로에서 시정수의 값이 클수록 과도현상의 소멸되는 시간은 길어진다.즉, 3. 단위 R = [Ω], L=[H] |
3) 시정수 |
스위치 인가시
따라서 시정수 |
4) R-L양단의 전압 |
|
|
[문제]
|
|
|
[풀이] R-L 직렬회로에서 스위치를
닫는 경우 전류 따라서 즉, 스위치를 닫은 후 시정수 만큼의 시간이 경과한 경우의 전류값은 정상전류의 63.2 %에 달한다. |
|
|
[문제]
|
|
|
[풀이] R-L 직렬회로이고 릴레이가 작동하면 회로가 구성되어 전류가 흐르므로
양변에 log10을 취하여 L에 관해 정리하면
따라서 |
|
|
|
|
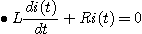
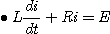
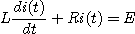
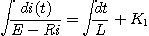 ,
, 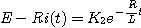
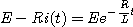
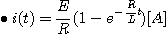
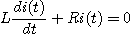
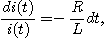 ln
ln 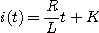
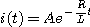
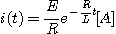
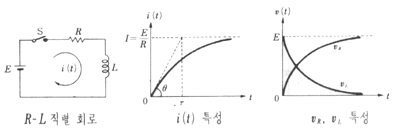
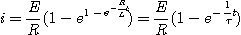 이므로 τ가 커지면,
이므로 τ가 커지면,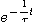 의 값이 증가하므로 과도상태는 길어진다.
의 값이 증가하므로 과도상태는 길어진다.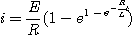
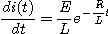
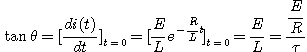
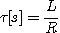
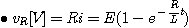
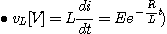
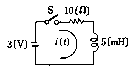 그림에서
스위치 S를 닫을 때 전류를
I(A)라 할 때 스위치를 닫는 순간부터 전류가
0.6321I[A]가
될 때까지의 시간[s]은 얼마인가? 단, 코일에는 에너지가 축적되어
있지 않다.
그림에서
스위치 S를 닫을 때 전류를
I(A)라 할 때 스위치를 닫는 순간부터 전류가
0.6321I[A]가
될 때까지의 시간[s]은 얼마인가? 단, 코일에는 에너지가 축적되어
있지 않다.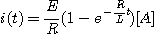 이고,
이고,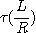 이 경과한 후의 전류
이 경과한 후의 전류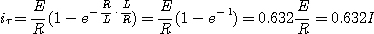
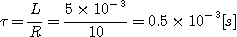
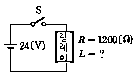 그림의
회로에서 릴레이의 동작전류는 10mA, 코일의 저항은 1200Ω, 인덕턴스
L[H] 이다.
그림의
회로에서 릴레이의 동작전류는 10mA, 코일의 저항은 1200Ω, 인덕턴스
L[H] 이다. 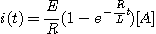 에서
에서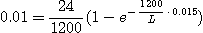
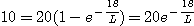
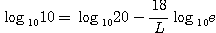 ,
, 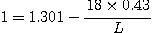
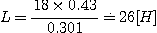
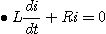
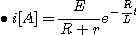 단 초기조건은
단 초기조건은 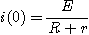
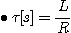
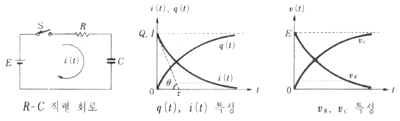
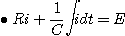
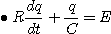
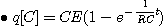
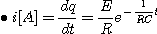
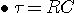
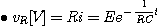
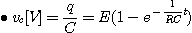
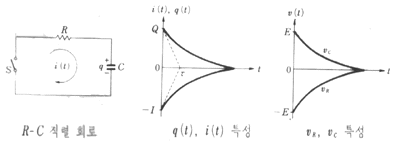
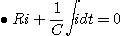
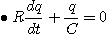
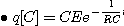
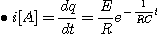 초기조건은 q(0)=Q=CE
초기조건은 q(0)=Q=CE 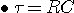
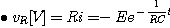
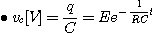
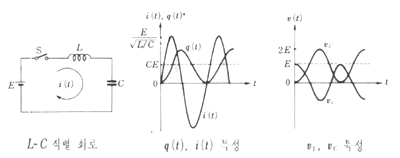
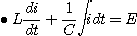
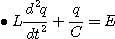
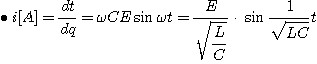
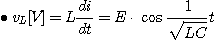
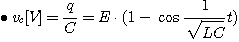
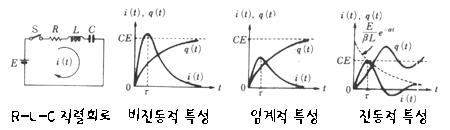
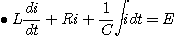
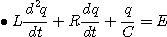
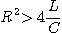
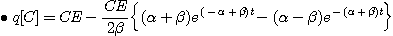
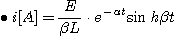
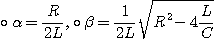
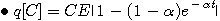
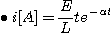 단,
단,